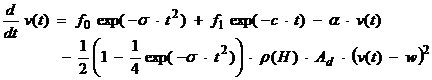A Model of Wind and Altitude Effects on 110-m Hurdles Joshua Spiegela, Jonas R
Mureikab Sportscience 7, sportsci.org/jour/03/jsjrm.htm, 2003
(4703 words)
|
|
Mathematical models that account for aerodynamic drag effects in the short sprints have been a subject of popular research for some time. Thus far, particular interest has been given to the short sprints, with major contributors including Davies (1980), Dapena and Feltner (1987), Keller (1974), Linthorne (1994), Mureika (2001, 2003) and Ward-Smith (1984, 1985, 1997, 1999). In this study we apply the four-component model of Mureika (2001), which includes mathematical terms representing physiological and physical effects, modified slightly to reflect differences in the 110‑m hurdle race. Mureika describes the sprinter’s equation of motion with four terms:
The first term is called the drive term, which will dominate during the first seconds of the race but then fall off due to the second-order exponential. The coefficient f0 is the magnitude of this term, as a force per unit mass. The value of s controls the severity of the exponential decay. Owing to constraints of the hurdle run, f0 is likely to be lower than the value found by Mureika (2001) for the 100 metre sprint. The second term is called the maintenance term, and describes the hurdler’s ability to consistently provide the same propulsive force. The coefficient f1 is a magnitude for this term (also as a force per unit mass), while c serves as a measure of the hurdler’s endurance. Differences in race format between hurdles and sprints should make f1 lower than the value used in Mureika’s (2001) example, whereas c should be slightly larger due to extra exertion in negotiating the hurdles. The third term is called the velocity term and provides an upper limit to the maximum speed attainable by a hurdler. It is based upon the principle that there must exist some limit set by physiological considerations. The coefficient α is responsible for the severity of this limit. In Mureika’s (2001) sprint model, stride rate was considered to be of importance. Vern Gambetta offers the following comments on hurdle strides in Brüggemann and Glad (1988): because of the placing of the hurdles, athletes are constrained to a certain running pattern. Between landing and the next takeoff, a male hurdler must complete three strides of between 1.88 and 1.99 m. This distance is substantially lower than the 2.5‑m average stride of the 100‑m sprinter. Since the hurdles present a unique constraint on stride length, the values for a found here will be somewhat higher than the value used in the sprint model. It should be noted that the dependence of hurdle performance on stride length could be a limitation of the applicability of the model. Ambient conditions will have a substantial effect on the athlete, and it would be reasonable to assume that the stride itself could be affected in ways not accounted for here. For this present study of our model, we will hold the stride pattern constant throughout the race. Finally, the last term in the model, the drag term, accounts for the force due to wind velocity and is modified by local air density and the cross-sectional area of the individual hurdler. The hurdle model will differ from the sprint model in that the cross-section of the hurdler is not constant (even approximately) throughout the race.. The coefficient Ad can be considered a drag per unit mass. For the purposes of the model, it was assumed that the cross-sectional area fell to about 60% of normal when the hurdler was mid-jump. Thus, using the value of Ad = 0.00288 m2 offered in Mureika (2001), Asmall = 0.00173 in Equation 2. It was assumed that the cross-section took on only two values, with the smaller being exposed for a typical hurdle clearance time on the order of 0.3 s (Müller, 1997). The coefficient r(H) is the air density as a function of altitude in g.cm‑3, the calculation of which is taken directly from Mureika (2001). It is expected that both this value, as well as the value for cross-section, will have a slightly greater effect on race time due to periods over which drag is the only force acting on the hurdler. This behavior is observed in the results. The term (n(t) – w)2 is the relative wind velocity in m.s‑1. Positive values of w indicate that the component of wind velocity parallel to the race is directed with the athlete, i.e. a tailwind. Note that as the value of w becomes more positive, the effect of drag becomes smaller. A headwind, indicated by a negative value of w, tends to increase the effect of drag in the model. When the hurdler is jumping, only the drag force is in action. Therefore, the other three forces are turned off periodically. We assumed that no significant additional force is needed to clear the hurdle, because the normal stride is sufficient to provide the proper lift. During the periods of hurdle clearance the equation of motion becomes
Each term in (1) and (2) is subject to certain coefficients, the appropriate values of which will be determined as described in the following section. We will then use these parameters in the model to simulate 110-meter hurdle performances under various wind and altitude conditions in order to determine by how much times are affected. These corrections will then be applied to the current top performance lists to study how such conditions have either helped or hindered record-setting races. We used numerical integration to solve the following pair of differential equations defining the motion of the athlete:
Equation (3) represents a general form of Equations (1) and (2), where the appropriate choice of (1) or (2) is adopted in the numerical integration algorithm. The reader will recognize Equations (3) and (4) as nothing more than equations of motion which can be solved for position x(t) and speed v(t). We have used the standard fourth-order Runge-Kutta-Fehlberg method with an initial time step of 0.05 s for the numerical integration (see e.g. Press 1993). For each step, the velocity and position were determined by solving the system of equations. When the position was equal to one of the hurdle locations, the equation for net force was modified as described in Equation 2. Gambetta described a typical hurdle stride, the distance between takeoff and landing, of 3.15 to 3.50 m (Brüggemann and Glad, 1988). This model makes use of a hurdle stride of the average of the two: 3.33 m. At each touchdown, time and velocity were recorded for later comparison with split times obtained from competitions. To determine the appropriate values for the coefficients of the model, code was developed in MATLAB to repeat the race up to 3000 times, incrementing each of the five coefficients in (1). At the conclusion of each modeled race, error was determined in the following manner: at each touchdown, the absolute difference between the observed time and that produced by the model was determined. The average of this difference across the ten touchdown times was then calculated. We took the error of the model to be this average deviation. The coefficients producing the minimum model error were then obtained. If one of the coefficient values was found to be at either extreme of the range over which it was being varied, the model was rerun with a new range of values for that coefficient. We have assumed that when the coefficient takes on such a limiting value, it is an indication that error is minimizing for values in that direction, but is prevented from doing so by the arbitrary range imposed. The model is run until a set of coefficients that fall within their respective ranges is found. Typically, more than one set of coefficients could produce the same error. For the data presented here, there were never more than five instances of the minimum error, but one trial run resulted in over forty. The coefficients associated with the minimum error were calculated. These values were then used to recalculate model error in the same manner as before, but based on the 0.01 s time step. The working assumption was that initial estimation via the 0.05 s time step allowed for a generally close fit, which was then to be improved by further variation in the coefficients. We found that a typical minimum model error for the initial runs was 0.015 to 0.020 s, which was widened to error in the range of 0.011 to 0.022 s after the decrease in step size. In other words, sometimes the fit from the 0.05 s time step was a good set for the more precise run but sometimes it was not. The set of coefficients producing the lowest error using the 0.01 s time step was reevaluated one final time to achieve further error minimization. For this run, the focus of the variation in coefficient values was smaller. For example, initial estimation for f0 might take place over the span 4.5 to 5.4 by increments of 0.1 and return a value of 5.0. In this case, the final estimation would take place over the smaller span 4.96 to 5.04 by increments of 0.02. The result was model error in the range of 0.010 to 0.018 s deviation for the data presented. Coefficient values between different runs tend to be fairly similar. In fact, for the three races we present here, all the variation in coefficient value is within about five of the initial estimation increments as described above. Further, trial runs on hurdle data produced a ~ 0.38 so consistently that it was fixed for the results presented here. This procedure was in line with the interpretation presented in Mureika (2001) that a is a physiological constant and as such should not change much from race to race. Consideration of
the consistency of the results lead to a decrease of the initial estimation
ranges around what can be considered expected values. While the result, in
some sense, was a pre-selection of the model coefficients (especially when it
has been shown that different sets of coefficients can produce the same
error), the similarity in race performance at the top levels of competition
allowed us to understand this result. At any rate, the actual values of the
coefficients have little inherent meaning, except perhaps in comparison
between individual athletes. It is the ability to study the effects of the
variation in the drag force the model provides that is of true interest.
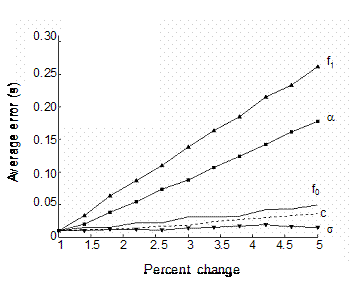
We have also investigated the model’s sensitivity to the values of the coefficients. From the accepted values for Greg Foster’s first run at the 1987 World Championship in Athletics (Brüggemann and Susanka, 1988), each coefficient was incremented up to 10% of its original value, with the others being held constant. The resulting change in model error is presented in Figure 1. For changes to f0, c, and s, the model error changes by less than 0.05 s. The effects of changes to f1 and a are more pronounced, with error changing to 0.26 and 0.18 s, respectively. These facts were taken into account for the final modifications of the estimation ranges, when it was expected that changes to one coefficient relative to another might play a more significant role in reducing the overall error. Touchdown data for the three hurdle performances by 1987 World Championship in Athletics gold medallist Greg Foster was collected from Brüggemann and Susanka (1988). His split times are presented alongside the model approximations in Table 1. Evidently, the model performs reasonably well in matching most of the split times, but the approach and run-in deviate from the observed values. Most noticeably, the true race time is up to 0.24 s faster than that produced by the model. The source of this error is the unrealistic velocity modeled after the final touchdown, for which corrections are discussed later. Note that for the presentation of the results, error is calculated as the deviation over the hurdle units only. This adjustment was made so that accurate fits to the touchdowns would not be sacrificed in the interest of obtaining slightly more realistic total race times.
The coefficients from the semi-final at
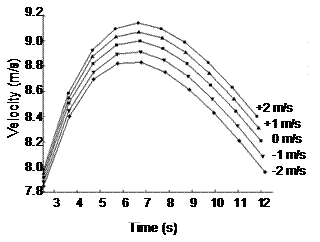
the 1987 WC run were used to model the race under five wind conditions,
ranging from –2.0 to 2.0 m.s‑1. Evidently, for a wind velocity
of 2 m.s‑1, the race time is shortened by 0.19 s. This
effect is roughly twice that observed in 100-m sprint models. The first plot in
Figure 2 demonstrates graphically the effects of wind velocity. With a change
of wind velocity from 2.0 to –2.0 m.s‑1, the maximum achievable race speed falls by 3.4%, from
9.14 to 8.83 m.s‑1. Through the opening portion of the race, wind velocity
does not play as large a role, but by the tenth touchdown, the extreme wind
values account for a difference in race speed of 0.44 m.s‑1. Thus the effects of drag on the athlete
accumulate through the race. The relative wind velocity is a constant in a
term partially describing the athlete’s acceleration. As the race goes on,
differences in wind velocity lead to more pronounced changes in performance.
Note that the plot is truncated in consideration of this effect in order to
better illustrate the variation in race speed. Also,
note that the plot demonstrates the relationship between the ten touchdown
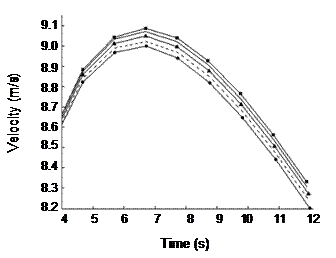
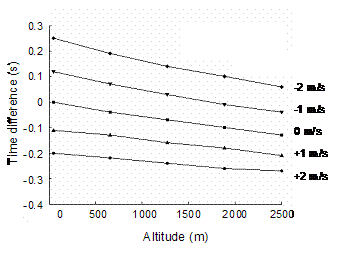
times and the speed at those specific times. Plotting the entirety of n(t) versus The coefficients from the semi-final of the 1987 WC run were also used to model the race at five altitudes, from sea level to 2500 meters. For each change in altitude of 625 m, the race time decreased by an average of 0.03 s. Note that even with relatively large changes in altitude, the effects on race time were much smaller than those of wind velocity. The second plot in Figure 2 is a graphical representation of the effects of air density. Clearly, the changes in maximum speed and race time are less substantial. With a change in altitude from 0 to 2500 m, the athlete’s top speed increases by only 1%, from 9.00 to 9.09 m.s‑1. As before, the effect compounds over time such that towards the end of the race there is a slightly greater gap between speeds. Figure 3 shows the corrections to finish time with increasing altitude for five wind velocities. The figure is a combination of the previous two analyses, demonstrating an increase to race time with more negative wind velocities and a decrease to race time with increasing altitude. The model demonstrates less effects of wind velocity at altitude, since the two factors are considered together in the equation of motion. Physically, the resistive capabilities of air are less, because density decreases with altitude. Notably, the effect of altitude is much more pronounced for opposing rather than contributing wind velocities. The implication is that altitude does more to erase the effects of opposing winds. Note that the first data points are slightly offset, because they were calculated for Rome and not for a true altitude of zero meters.
The ability to correct race times for the effects of wind velocity and altitude provides an opportunity to reexamine the record books with all races reported as if they were run at sea level with no wind. Races with recorded wind velocity of 2 m.s‑1 or greater are deemed wind-assisted and are not included among the official top finishes. However, examination of the record books for the 110‑m hurdles reveals considerable variation in wind velocities even among twelve best official times (ranked 1-9) (Larsson, 2003). The results presented in the previous sections suggest that correction for this variation could lead to a significant restructuring of the record books. Tables 2 and 3 below display the top legal and non-legal (wind-assisted) finishes on record for the men’s 110‑m hurdle (Larsson, 2003). For each entry, a characteristic model race was run under the wind and altitude conditions noted to determine a correction to the official time. This method assumes enough similarity among the athletes to allow subjecting them to the same corrections as the characteristic model hurdler. Notably, several of the fastest times among the non-legal records are modified to more typical times under the zero wind conditions, revealing the large positive effect of wind assistance. Table 4 displays the predicted restructuring of the records, based on the model corrections presented. Notice that the former ninth best finish, by Colin Jackson in Sestriere, is now first. This result is particularly interesting, because that particular record is marked for having taken place at an altitude of 2065 m. The modification reveals that the 1.60 m.s‑1 headwind Jackson faced in this event was far more significant than the altitude. Meanwhile, the former best finish falls to seventh, due largely to the 0.50 m.s‑1 wind that is predicted to have improved the finish time by roughly 0.06 s. No non-legal results are added to the restructured list in Table 4, with the 12.87 s recorded result for Roger Kingdom modified to 13.15 s. Also note that the two eighth best finishes, both recorded by Allen Johnson in Atlanta, are separate races holding places two and eight in Table 2.
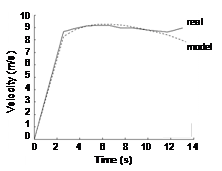
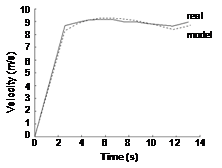
Although the model has been able to match the split times adequately well, finish time has consistently been off. It seems clear that the velocities created by the model may be unrepresentative of real races. Even speaking empirically, the speed curve modeled here decreases after the maximum is reached, while real hurdle athletes increase their speed for the final portion of the race. For the 1987 IAAF World Championships (hereafter WC) data that was the subject of most analysis, there were no wind velocity data available, so we assumed that well-matched split times indicated well-matched velocities. The 1997 WC in Athens did include instantaneous speed data for the top four finishers, so we had an opportunity to match the model to real results. Figure 4 shows that while the model velocity closely approximates the observed velocity for most of the race, the two begin to diverge in the closing moments. To approximate a correction, we considered that the observed increase in speed at the end of the race was due to constraints on running being released. That is to say, the run-in is an open sprint to which the hurdle considerations do not apply. Therefore, we modified the model procedure to decrease the value for a after the final touchdown, representing a relaxation of the physiological constraint of stride length. Some guess and check was employed to find a value for a that resulted in apparently parallel velocity curves on the run in, indicating equal acceleration through the end of the race. Figure 4 shows the corrected model velocity, with a value for a of 0.292 substituted after the 10th touchdown. The coefficient a could of course be adjusted to reach the proper race time and easily fit into the error reducing scheme as it exists now. However, such an approach would tend to create an unrealistic acceleration. It would therefore be necessary to error check against speed in the run-in, to obtain model splits that are still well-matched to the race.
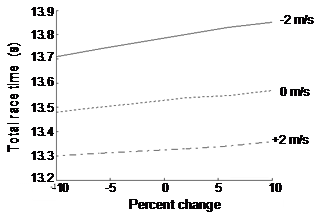
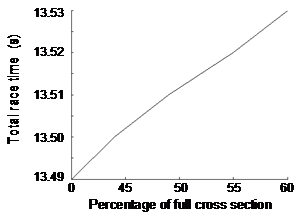
As noted in the Introduction, we have suggested a range of values for the drag coefficient and the cross-sectional area of the hurdler. Moreover, the analysis performed herein was based upon assumptions about an average athlete. It would be possible, of course, to accurately measure the height and weight of individual athletes and use these values to determine a more accurate value for Ad. With that in mind, an attempt was made to determine the effect of variation in Ad on race time. Figure 5 shows the effect when Ad was 10% larger or smaller. The result is a 0.14 s increase in race time from the minimum value of Ad to the maximum when the athlete faces a headwind of –2 m.s‑1. For a tailwind of the same magnitude, there is only a 0.06 s increase in race time. It is also presumed that the ratio of Asmall to Ad has some bearing on race performance. The estimation of 60% was based upon brief examination of hurdling photos, but no data could be located specifically addressing the change in cross-sectional area during hurdle clearance. Initial guesses had placed the ratio as low as 40%, and Figure 6 demonstrates variation in total race time for a range of ratios. The result is a fairly small deviation, with an increase to total race time of 0.04 s over the range of values for Asmall.
We have shown that the 110‑m hurdle race can be reasonably modeled using a modified version of an established 100‑m sprint model. Mid-race touchdown times are consistently matched within an average error of less than 0.02 s. Sources of error towards the end of the race can be accounted for, and the availability of full race data could make determining the proper corrections easier. The effect of wind velocity is perhaps unexpected, in that it is about twice that observed in sprint races. However, it is easily reconciled with an increased influence of drag during hurdle clearance. Better determination of model parameters such as drag area or propulsive forces can help determine the validity of these predictions. Link to reviewer's comment. JS would like to thank James Higdon for insightful discussions. JRM acknowledges Canada’s Natural Sciences and Engineering Research Council (NSERC) for additional research funding. Brüggemann P, Susanka P (1988). Scientific report on the second IAAF world championships in athletics, Rome, 1987. International Athletic Foundation, London Brüggemann G, Glad B (editors) (1988). Scientific research project at the game of the XXIVth Olympiad – Seoul 1988. IAAF and Charles University, Prague Davies CTM (1980). Effects of wind assistance and resistance on the forward motion of a runner. Journal of Applied Physiology 48: 702-709 Dapena J, Feltner M (1987). Effects of wind and altitude on the times of 100-meter sprint races. International Journal of Sport and Biomechanics 3, 6-39 Keller JB (1974). Optimal velocity in a race. American Mathematical Monthly 81, 474-480 Linthorne N.P. (1994). The effect of wind on 100-m sprint times. Journal of Applied Biomechanics 10, 110-131 Larsson P (2003). Track and field all time performances homepage. http://taf.sport.nu/men.htm Müller H, Hommel H (editors) (1997). Biomechanical research project at the VIth world championships in athletics, Athens 1997. New Studies in Athletics. 13(2-3), 51 Mureika JR (2001). A realistic quasi-physical model of the 100‑m dash. Canadian Journal of Physics 79, 697-713 Mureika, JR (2003). Modeling wind and
altitude effects in the 200-m sprint.
Canadian Journal of Physics 81, 895-910 Press, WH, Flannery, BP, Teukolsky, SA, Vetterling, WT, (1993). Numerical Methods in C: The Art of Scientific Computing (2nd edition). Cambridge University Press, Cambridge Ward-Smith A J (1984). Air resistance and its influence on the biomechanics and energetics of sprinting at sea level and at altitude. Journal of Biomechanics 17, 339-347 Ward-Smith AJ (1985). A mathematical analysis of the influence of adverse and favourable winds on sprinting. Journal of Biomechanics 18, 351-357 Ward-Smith, A.J (1997). A mathematical analysis of the bioenergetics of hurdling, Journal of Sport Sciences 15, 517-526 Ward-Smith, A.J (1999). New insights into the effect of wind assistance on sprinting performance. Journal of Sport Sciences 17, 325-334 Published Dec 2003 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||