|
A New View of Statistics |
|
I've already defined statistical significance in terms of confidence intervals. The other approach to statistical significance--the one that involves p values--is a bit convoluted. First you assume there is no effect in the population. Then you see if the value you get for the effect in your sample is the sort of value you would expect for no effect in the population. If the value you get is unlikely for no effect, you conclude there is an effect, and you say the result is "statistically significant".
Let's take an example. You are interested in the correlation between two things, say height and weight, and you have a sample of 20 subjects. OK, assume there is no correlation in the population. Now, what are some unlikely values for a correlation with a sample of 20? It depends on what we mean by "unlikely". Let's make it mean "extreme values, 5% of the time". In that case, with 20 subjects, all correlations more positive than 0.44 or more negative than -0.44 will occur only 5% of the time. What did you get in your sample? 0.25? OK, that's not an unlikely value, so the result is not statistically significant. Or if you got -0.63, the result would be statistically significant. Easy!
But wait a minute. What about the p value? Yes, umm, well... The problem is that stats programs don't give you the threshold values, ±0.44 in our example. That's the way it used to be done before computers. You looked up a table of threshold values for correlations or for some other statistic to see whether your value was more or less than the threshold value, for your sample size. Stats programs could do it that way, but they don't. You want the correlation corresponding to a probability of 5%, but the stats program gives you the probability corresponding to your observed correlation--in other words, the probability of something more extreme than your correlation, either positive or negative. That's the p value. A bit of thought will satisfy you that if the p value is less than 0.05 (5%), your correlation must be greater than the threshold value, so the result is statistically significant. For an observed correlation of 0.25 with 20 subjects, a stats package would return a p value of 0.30. The correlation is therefore not statistically significant.
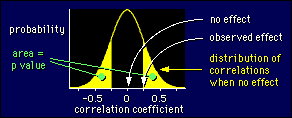
Phew! Here's our example summarized in a diagram:
The curve shows the probability of getting a particular value of the correlation in a sample of 20, when the correlation in the population is zero. For a particular observed value, say 0.25 as shown, the p value is the probability of getting anything more positive than 0.25 and anything more negative than -0.25. That probability is the sum of the shaded areas under the probability curve. It's about 30% of the area, or a p value of 0.3. (The total area under a probability curve is 1, which means absolute certainty, because you have to get a value of some kind.)
Results falling in that shaded area are not really unlikely, are they? No, we need a smaller area before we get excited about the result. Usually it's an area of 5%, or a p value of 0.05. In the example, that would happen for correlations greater than 0.44 or less than -0.44. So an observed correlation of 0.44 (or -0.44) would have a p value of 0.05. Bigger correlations would have even smaller p values and would be statistically significant.
![]() Test
Statistics
Test
Statistics
The stats program works out the p value either
directly for the statistic you're interested in (e.g. a correlation), or for a
test statistic that has a 1:1 relationship with the effect statistic. A test statistic
is just another kind of effect statistic, one that is easier for statisticians
and computers to handle. Common test statistics are t, F, and chi-squared. You
don't ever need to know how these statistics are defined, or what their values
are. All you need is the p value, or better still, the confidence limits or interval
for your effect statistic.
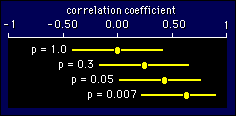 --that
getting a p value of less than 0.05 is the same as having a 95%
confidence interval that doesn't overlap zero. I won't try to explain
it, other than to say that you have to slide the confidence interval
sideways to prove it. But make sure you are happy with this figure,
which shows some examples of the relationship between p values and
95% confidence intervals for observed correlations in our example of
a sample of 20 subjects.
--that
getting a p value of less than 0.05 is the same as having a 95%
confidence interval that doesn't overlap zero. I won't try to explain
it, other than to say that you have to slide the confidence interval
sideways to prove it. But make sure you are happy with this figure,
which shows some examples of the relationship between p values and
95% confidence intervals for observed correlations in our example of
a sample of 20 subjects.
The relationship between p values and confidence intervals also provides us with a more sensible way to think about what the "p" in "p value" stands for. I've already said that it's the probability of a more extreme (positive or negative) result than what you observed, when the population value is null. But hey, what does that really mean? I get lost every time I try to wrap my brain around it. Here's something much better: if your observed effect is positive, then half of the p value is the probability that the true effect is negative. For example, you observed a correlation of 0.25, and the p value was 0.30. OK, the chance that the true value of the correlation is negative (less than zero) is 0.15 or 15%; or you can say that the odds of a negative correlation are 0.15:0.85, or about 1 to 6 (1 to 0.85/0.15). Maybe it's better to it turn around and talk about a probability of 0.85 (= 1 - p/2), or odds of 6 to 1, that the true effect is positive. Here's another example: you observed an increase in performance of 2.6%, and the p value was 0.04, so the probability that performance really did increase is 0.98, or 49 to 1. Check your understanding by working out how to interpret a p value of exactly 1.
So, if you want to include p values in your next paper, here is a new way to describe them in the Methods section: "Each p value represents twice the probability that the true value of the effect has any value with sign opposite to that of the observed value." I wonder if reviewers will accept it. In plain language, if you observe a positive effect, 1 - p/2 is the probability that the true effect is positive. But even with this interpretation, p values are not a great way to generalize an outcome from a sample to a population, because what matters is clinical significance, not statistical significance.
I have now included the calculations in the spreadsheet for confidence limits and likelihoods. I've called the smallest clinically important value a "threshold value for chances [of a clinically important effect]". You have to choose a threshold value on the basis of experience or understanding. You also have to include the observed value of the statistic and the p value provided by your stats program. For changes or differences between means you also have to provide the number of degrees of freedom for the effect, but the exact value isn't crucial. The spreadsheet then gives you the chances (expressed as probabilities and odds) that the true value is clinically positive (greater than the smallest positive clinically important value), clinically negative (less than the negative of the smallest important value), and clinically trivial (between the positive and negative smallest important values). The spreadsheet also works out confidence limits, as explained in the next section below.
Use the spreadsheet to play around with some p values, observed values of a statistic, and smallest clinically important values to see what the chances are like. I've got an example there showing that a p value of 0.20 can give chances of 80%, 15% and 5% for clinically positive, trivial, and negative values. Wow! It's clear from data like these that editors who stick to a policy of "publishable if and only if p<0.05" are preventing clinically useful findings from seeing the light of day.
I have written two short articles on this topic at the Sportscience site. The first article introduces the topic, pretty much as above. The second article summarizes a Powerpoint slide show I have been using for a seminar with the title Statistical vs Clinical or Practical Significance, in which I explain hypothesis testing, P values, statistical significance, confidence limits, probabilities of clinical significance, a qualitative scale for interpreting clinical probabilities, and some examples of how to use the probabilities in practice. Download the presentation (91 KB) by (right-)clicking on this link. View it as a full slide show so you see each slide build.
![]() Confidence
Limits from a P Value
Confidence
Limits from a P Value
Stats programs often don't give you confidence
limits, but they always give you the p value. So here's a clever way to derive
the confidence limits from the p value. It works for differences between means
in descriptive or experimental studies, and for any normally distributed statistic
from a sample. Best of all, it's on a spreadsheet! I explain how it works in the
next paragraph, but it's a bit tricky and you don't have to understand it to use
the spreadsheet. Link back to the previous
page to download the spreadsheet.
I'll explain with an example. Suppose you've done a controlled experiment on the effect of a drug on time to run 10,000 m. Suppose the overall difference between the means you're interested in is 46 seconds, with a p value of 0.26. From the definition of the p value (see top figure on this page), we can draw a normal probability distribution centered on a difference of 0 seconds, such that there is an area of 0.26/2 = 0.13 to the right of 46 and a similar area to the left of -46. Or to put it another way, the area between -46 and 46 is 1-0.26 = 0.74. If we now shift that distribution until it's centered over 46, it represents the probability distribution for the true value. We know that the chance of the true value being between 0 and 92 is 0.74, so now all we need is the range that will make the chance 0.95, and that will be our 95% confidence interval. To work it out, we use the fact that the distribution is normal. That allows us to calculate how many standard deviations (also known as the z score) we have to go on each side of the mean to enclose 0.74 of the area under the normal curve. We get that from tables of the cumulative normal distribution, or the function NORMSINV in an Excel spreadsheet. Answer: 1.13 standard deviations. Ah, but we know that 1.96 standard deviations encloses 95% of the area, and because the 1.13 standard deviations represents 46 seconds, our confidence interval must be -46(1.96/1.13) to +46(1.96/1.13), i.e. -34 to +126.
Fine, except that it's not really a normal distribution. With a finite number of subjects, it's actually a t distribution, so we have to use TINV in Excel. What's more, the 95% confidence limits are really a titch more than 1.96 standard deviations each side of the mean. Exactly how much more depends on the number of subjects, or more precisely, the number of degrees of freedom. With your own data, search around in the output from the analysis until you find the degrees of freedom for the error term or the residuals. Put it into the spreadsheet, along with the observed value of the effect statistic, and its p value (not the p value for the model or for an effect in the model, unless it is the statistic). If you can't find the number of degrees of freedom on the output, the spreadsheet tells you how to calculate it. And if you don't get it exactly right, don't worry: the confidence limits hardly change for more than 20 degrees of freedom.
![]() One
Tail or Two?
One
Tail or Two?
Notice in the first figure on this page that
the p value is calculated for both tails of the distribution of the statistic.
That follows naturally from the meaning of statistical significance, and it's
why tests of significance are sometimes called two tailed. In principle
you could eliminate one tail, double the area of other tail, then declare statistical
significance if the observed value fell within the one-tailed area. The result
would be a one-tailed test. Your Type I error rate would still be 5%, but
a smaller effect would turn out to be statistically significant. In other words,
you would have more power to detect the effect.
So how come we don't do all tests as one-tailed tests? Hmm... The people who support the idea of such tests--and they are a vanishing breed--argue that you can use it to test for, say, a positive result only if you have a good reason for believing beforehand that the outcome will be positive. I hope I am characterizing their position correctly, because I don't understand it. What is a "good reason"? It seems to me that you would have to be absolutely certain that the outcome would be positive, but in that case running the test for statistical significance is pointless! I therefore don't buy into one-tailed tests. If you have any doubts, revert to the confidence-interval view of significance: one-sided confidence intervals just don't make sense, but confidence limits equally placed on each side of the observed value is unquestionably a correct view.
Except that... there is a justification for one-tailed tests after all. You just interpret the p value differently. P values for one-tailed tests are half those for two-tailed tests. It follows that the p value from a one-tailed test is the exact probability that the true value of the effect has opposite sign to what you have observed, and 1 - p is the probability that the true value of the effect has the same sign, as I explained above. Hey, we don't have to muck around with p/2. So here's what you could write in the Methods section of your paper: "All tests of significance are one-tailed in the direction of the observed effect. The resulting p values represent the probability that the true value of the effect is of sign opposite to the observed value." Give it a go and see what happens. Such a statement would be anathema to reviewers or statisticians who assert that an observed positive result is not a justification for doing a one-tailed test for a positive result. They would argue that you are downgrading the criterion for deciding what is "statistically significant", because you are effectively performing tests with a Type I error of 10%. Fair enough, so don't mention statistical significance at all. Just show 95% confidence limits, and simply say in the Methods: "Our p values, derived from one-tailed tests, represent the probability that the true value of the effect is of sign opposite to the observed value."
But as I discussed above, the probability that an effect has a substantially positive (or negative) value is more useful than the probability that the effect has any positive (or negative) value. Confidence limits are better than one-tailed p values from that point of view, which is why you should always include confidence limits.
Some researchers and statisticians claim that a decision has to be
made about whether a result is statistically significant. According
to this logic, if p is less than 0.05 you have a publishable result,
and if p is greater than 0.05, you don't. 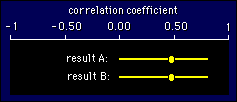 Here's
a diagram showing the folly of this view of the world. One of these
results is statistically significant (p<0.05), and the other isn't
(p>0.05). Which is publishable? Answer: both are, although you'd
have to say in both cases that more subjects should have been tested
to narrow down the likely range of values for the correlation. And in
case you missed the point, the exact p values are 0.049 and 0.051.
Don't ask me which is which!
Here's
a diagram showing the folly of this view of the world. One of these
results is statistically significant (p<0.05), and the other isn't
(p>0.05). Which is publishable? Answer: both are, although you'd
have to say in both cases that more subjects should have been tested
to narrow down the likely range of values for the correlation. And in
case you missed the point, the exact p values are 0.049 and 0.051.
Don't ask me which is which!
Some journals persist with the old-fashioned practice of allowing authors to show statistically significant results with p<0.05 or p<0.01, and non-significant results with p>0.05. Exact p values convey more information, but confidence intervals give a much better idea of what could be going on in the population. And with confidence intervals you don't get hung up on p values of 0.06.
![]() Hypothesis
Testing
Hypothesis
Testing
The philosophy of making a decision
about statistical significance also spawned the practice of
hypothesis testing, which has grown to the extent that some
departments make their research students list the hypotheses to be
tested in their projects. The idea is that you state a null
hypothesis (i.e. that there is no effect), then see if the data
you get allow you to reject it. Which means there is no effect until
proved otherwise--like being innocent until proved guilty. This
philosophy comes through clearly in such statements as "let's see if
there is an effect".
What's wrong here? Well, people may be truly innocent, but in nature effects are seldom truly zero. You probably wouldn't investigate something if you really believed there was nothing going on. So what really matters is estimating the magnitude of effects, not testing whether they are zero. But that's only a philosophical issue. There are more important practical issues. Getting students to test hypotheses diverts their attention from the magnitude of the result to the magnitude of the p value. Read that previous sentence again, please, it's that important. So when a student researcher gets p>0.05 and therefore "accepts the null hypothesis", s/he usually concludes erroneously that there is no effect. And if s/he gets p<0.05 and therefore "rejects the null hypothesis", s/he still has little idea of how big or how small the effect could be in the population. In fact, most research students don't even know they are supposed to be making inferences about population values of a statistic, even after they have done statistics courses. That's how hopelessly confusing hypothesis testing and p values are.
"Let's see if there is an effect" isn't too bad, if what you mean is "let's see if there is a non-trivial effect". That's what people really intend. But a test for statistical significance does not address the question of whether the effect is non-trivial; instead, it's a test of whether the effect is greater than zero (for an observed positive effect). And it's easy to get a statistically significant effect that could be trivial, so hypothesis testing doesn't do a proper job. With confidence limits you can see immediately whether the effect could be trivial
Research questions are more important than research hypotheses. The right question is "how big is the effect?" And I don't just mean the effect you observe in your sample. I mean the effect in the population, so you will have to show confidence limits to delimit the population effect.
![]() Using
P Values
Using
P Values
When I first published this book, I
was prepared to concede that p values have a use when you report lots
of effects. For example, with 20 correlations in a table, the ones
marked with asterisks stand out from the rest. Now I'm not so sure
about the utility of those asterisks. The non-significant results
might be just as interesting. For example, if the sample size is
large enough, a non-significant result means the effect can only be
trivial, which is just as important as the effect being substantial.
And if the sample size isn't large enough, a non-significant result
with the lower confidence limit in the trivial region
(e.g. r = 0.34, 95%CL = -0.03 to 0.62) is
arguably only a tad less interesting than a statistically significant
result with the lower confidence limit still in the trivial region
(e.g. r = 0.38, 95%CL = 0.02 to 0.65). So I think
I'll harden my attitude. No more p values.
By the way, if you do report p values with your outcome
statistics, there is no point in reporting the value of the test
statistic as well. It's superfluous information, and few people know
how to interpret the magnitude of the test statistic anyway. But you
must make sure you give confidence limits or exact p values,
and describe the statistical modeling procedure in the Methods
section.
Go to: Next
· Previous
· Contents
· Search
· Home
webmaster=AT=sportsci.org
· Sportsci
Homepage
Last updated 29 April 02