model: nominal <= numeric
example: sport <= height
|
A New View of Statistics | |
![]() Categorical Modeling
Categorical Modeling
model:
nominal <= numeric
example: sport <= height
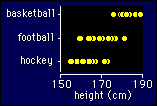 Another name for
this model is discriminant function analysis, because, for
example, you end up with a function of height that allows you to
predict which sport a person belongs in. Whether the person would do
better in that sport is another question requiring different
variables, of course!
Another name for
this model is discriminant function analysis, because, for
example, you end up with a function of height that allows you to
predict which sport a person belongs in. Whether the person would do
better in that sport is another question requiring different
variables, of course!
This model is the least common of the four. It's much easier to turn the model around to make it height <= sport, and apply... what? Yes, an ANOVA. Strictly speaking, though, if the research calls for height to be the independent variable, then you should apply categorical modeling, and express your outcomes as an effect of height on the probability of being in the different sports. You end up with horrible outcome measures like an odds ratio per unit of height, which blows away everyone except card-carrying statisticians! By the way, the test statistic is chi-squared.
Another approach is to treat each sport as a separate variable, then code the value as 1 if the person belongs to the sport and 0 if not. You can also group the sports in some sensible way and again code a variable as 0 or 1 if the person belongs to that group. You then treat these variables as numeric and analyze them in the usual way. You have to assume the sample size is big enough to ensure the sampling distribution of the outcome statistic is normal. I explain what all this means shortly.
A special case of categorical modeling is logistic regression. You have to use this model when the dependent variable is ordinal. A page devoted to this problem also comes up shortly. You could also turn simple models like these around and analyze them as ANOVAs, but you shouldn't.
Next, some details about how a
stats program fits a model.
Go to: Next · Previous · Contents · Search
· Home
editor
Last updated 9 June 2003