|
A New View of Statistics |
|
| Go to: Next
· Previous
· Contents
· Search
· Home
|
|
People hate numbers, and they can't understand them in bulk. That's why you have to summarize data when you present results of your research. You probably know most of the peaks on this part of the statistical map already: frequency distributions, simple statistics like the mean and standard deviation, effect statistics like correlation coefficients, and so on. You may not have attempted to master things like effect size, relative frequencies and risks, a scale of magnitudes for effects, dimension reduction, validity, reliability, and the finer points of how many digits to use, but they're all easy enough.
The only other big feature on the statistical map is generalizing to a population. That's where you use a bunch of numbers from a few subjects to make inferences about everyone's numbers. More about that later.
![]() BASICS
BASICS
I said usually a set of numbers, because some data are a set of labels, names, or levels. Again, when these labels represent the same kind of thing, that thing is a variable. For example, the labels male and female are values for the variable sex. Variables with numbers as values are called numeric; variables with names or labels as values are called nominal, for obvious reasons.
Numeric variables come in several varieties. Things like height and weight are the usual kind. These can have just about any value to as many decimal places as we like, so we call them continuous. An example of a variable that is not continuous is a count, such as the number of injuries a person has experienced.
One other kind of variable can't decide whether it's numeric or nominal. A good example is competitive level, with values of novice, club, national, international. There is an obvious order in the levels: novice is at the bottom, club is next, and so on, so we call the variable ordinal. It's usual to recode each level with an integer (1=novice, 2=club, 3=national, 4=international).
Here is an example of a data set with three nominal variables, two continuous numeric variables, one ordinal variable, and one counting variable:
|
subject
|
|
|
|
|
|
|
|
AJH
|
|
|
|
|
|
|
|
CJD
|
|
|
|
|
|
|
|
NIH
|
|
|
|
|
|
|
|
ERF
|
|
|
|
|
|
|
|
MBA
|
|
|
|
|
|
|
Each row in the data set represents the values of all the variables for one subject. It's called an observation. You can have missing values in the data set, too, as shown.
Data for more than a few subjects and variables have to be
summarized to make them palatable. You can't trot out the whole data
set every time you want to talk about it.
![]() Frequency
Distributions
Frequency
Distributions
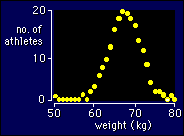 For
numeric variables, one important way to summarize the values is to
graph them as a frequency distribution. Here's what the
weights of 200 athletes might look like in a frequency distribution
done as a scatter plot, which shows a point for the number of
times each weight occurs.
For
numeric variables, one important way to summarize the values is to
graph them as a frequency distribution. Here's what the
weights of 200 athletes might look like in a frequency distribution
done as a scatter plot, which shows a point for the number of
times each weight occurs.
You can also show the frequencies as vertical bars rather than points, in which case the figure is called a histogram. Most stats programs also have a clever way to show the values as a kind of histogram called a stem-and-leaf plot. When you see one it will be obvious what is going on.
It's normal for data to have a symmetrical bell-shaped frequency distribution like the one shown. Hence the name: the normal distribution. Exactly why most things are normally distributed is a bit of a mystery.
When you have lots of values for a variable, it's a good idea to get a stats program to do a frequency distribution or stem-and-leaf plot, so you can see if there are any obviously wrong outliers. Outliers are often just errors in data entry. It might be worth checking out the original data for the person on 50 kg in the above figure. You certainly would if the value was 40 kg. Even if the value is correct, you might have a good reason to exclude that observation.
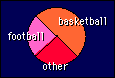 Summarizing
the values of a nominal variable like sex is a simple matter. All you
need is the frequency of each level. For example, a group of athletes
might consist of 101 basketballers, 49 footballers, and 51 others.
One occurrence of the new sport footbull would be an example of an
outlier in need of correction. You can display the frequencies
graphically as proportions in a pie chart, as shown, or as a
bar divided up in the right proportions. Pie charts seem to be
frowned on in scientific publications, but you see them in
magazines.
Summarizing
the values of a nominal variable like sex is a simple matter. All you
need is the frequency of each level. For example, a group of athletes
might consist of 101 basketballers, 49 footballers, and 51 others.
One occurrence of the new sport footbull would be an example of an
outlier in need of correction. You can display the frequencies
graphically as proportions in a pie chart, as shown, or as a
bar divided up in the right proportions. Pie charts seem to be
frowned on in scientific publications, but you see them in
magazines.
![]() Probability
Probability
Probability is obviously a number between 0 and 1. When it's 0, there's no way you'll be successful, and when it's 1 you'll win every time. You can't have negative probability.
We can represent probability in several other ways. In the above example, we can talk about 1 chance in 6, 17 times in 100, 17%, a likelihood of 0.17, or 17% likely. You'll also meet odds of 1 to 5, which means 1 success for every 5 failures. Odds of 1 to 1 means a 50% chance of something happening (as in tossing a coin and getting a head), and odds of 99 to 1 means it will happen 99 times out of 100 (as in bad weather on a public holiday).
A probability distribution is just a frequency
distribution with each frequency divided by the total number of
observations. It follows (although it's not obvious) that the area
under a probability distribution has something to do with the
probability of getting certain numbers. In the above example of the
distribution of people's weights, if you draw someone at random from
the population; the chance that they will have a weight between 60
and 70 kg is the area under the curve between 60 and 70 kg. What's
more, the total area under a probability distribution is 1. Hmm...
Too academic. Too technical. Not essential. But you will need
to feel comfortable with probability when we deal with p
value, confidence limits,
relative risk and odds ratio.
![]() Statistics
Statistics
Let's start with simple statistics. The simplest of all is a
count of the number of numbers or levels, also known as
sample size. That's as far as it goes for a nominal variable.
For numeric variables, we usually use two more simple statistics to
give people an idea of what the original numbers are like: a
statistic to represent the middle values of the data (on the
next page), and a statistic to show how the
data are spread out (on following
pages).
Go to: Next
· Previous
· Contents
· Search
· Home
webmaster=AT=sportsci.org
·
Sportsci
Homepage
·
Copyright
©1997
Last updated 15 April 00