Summarizing
Data:
SIMPLE STATISTICS & EFFECT STATISTICS continued
 EFFECT STATISTICS
EFFECT STATISTICS
All the statistics we've met so far summarize
a set of values of a single variable. But it's possible to have statistics describing
the relationship between two or more sets of numbers. These are the statistics
that really matter in research.
There is no agreed generic name for these statistics. I've seen measures
of effect in the literature, so let's call them effect statistics.
The effect refers to the idea that one variable has an effect on another.
The main effect statistics are the difference in means (this page),
the correlation coefficient (next page)
and relative frequency (following page). Each
of these effect statistics comes in several varieties, I close this section
with a page on a scale of magnitudes for
effect statistics
 Difference in Means
Difference in Means
Sometimes you
can express the finding of a study simply as a difference between the means of
two groups, in the original raw units of measurement. For example, a group of
elite male runners has a mean body mass of 66.4 kg, whereas a subelite group weighs
in with an average of 68.5. The difference of 2.1 kg is the effect.
Depending on the variable, you often want to talk about the difference between
means as a percent difference. In the above example, you could say that
the subelite runners are 3.2% heavier than the elites (2.1/66.4 = 0.032 = 3.2%).
Percent differences are a natural way to express differences in the mean of
variables that need log transformation. Percent
effects are particularly appropriate for measures of athletic performance.
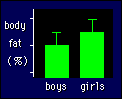 Converting the difference to
a percent is one way to make the difference dimensionless, and therefore
more generic. Another important way is to express the difference as a fraction
or multiple of a standard deviation. Work out the difference between the means,
then divide it by the average standard deviation for the two groups. What you
end up with is the standardized difference in the means, a number that represents "how
many standard deviations" the two groups differ by. Look closely at the imaginary
example in the figure and work out the effect size for the difference in body
fat between boys and girls. Answer: one unit, or 1.0, or one standard deviation.
Note that the unit of measurement for body fat is irrelevant. I've shown it
as the usual % of body mass, but it could be kg or pounds--the effect-size statistic
has the same value. The effect-size statistic is appropriate for studies of
population health, where differences or changes in means that impact the average
person are paramount.
Converting the difference to
a percent is one way to make the difference dimensionless, and therefore
more generic. Another important way is to express the difference as a fraction
or multiple of a standard deviation. Work out the difference between the means,
then divide it by the average standard deviation for the two groups. What you
end up with is the standardized difference in the means, a number that represents "how
many standard deviations" the two groups differ by. Look closely at the imaginary
example in the figure and work out the effect size for the difference in body
fat between boys and girls. Answer: one unit, or 1.0, or one standard deviation.
Note that the unit of measurement for body fat is irrelevant. I've shown it
as the usual % of body mass, but it could be kg or pounds--the effect-size statistic
has the same value. The effect-size statistic is appropriate for studies of
population health, where differences or changes in means that impact the average
person are paramount.
The standardized difference in the means is sometimes known simply as the effect-size statistic, although this term confuses the concept with the magnitude of other kinds of effect.
A page on this topic comes up shortly. Meanwhile,
to get you thinking about it, how big is the effect shown in the above figure?
This difference of one standard deviation has been regarded as large,
although I now think it's only a moderate effect. Anything less than
0.2 standard deviations isn't worth worrying about.
The example above is for two groups of subjects, but you should
also use the concept of effect size when looking at changes in the
mean as a result of an experiment. For example, the above two bars
could represent muscle mass before and after treatment with anabolic
steroids. In this case you use the SD of the pre scores only to
standardize the effect. (I'd figured this out years ago, but until Oct 06 I missed a mistaken assertion on this page that you average the pre and post SDs. Sorry about that.) Some people think mistakenly that you
should use the SD of the change scores to standardize effects in experiments. If you have a control
group as well, you use the
SD of all the pre scores, and you subtract the change
in the control group from the change in the experimental group to get
the magnitude of the experimental effect.
When you understand effect sizes, you'll know why you should
always show standard deviations rather than standard errors of the
mean with means. See the page devoted this
important issue.
Go to: Next · Previous · Contents · Search
· Home
Last updated 2 Oct 06
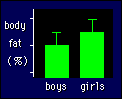 Converting the difference to
a percent is one way to make the difference dimensionless, and therefore
more generic. Another important way is to express the difference as a fraction
or multiple of a standard deviation. Work out the difference between the means,
then divide it by the average standard deviation for the two groups. What you
end up with is the standardized difference in the means, a number that represents "how
many standard deviations" the two groups differ by. Look closely at the imaginary
example in the figure and work out the effect size for the difference in body
fat between boys and girls. Answer: one unit, or 1.0, or one standard deviation.
Note that the unit of measurement for body fat is irrelevant. I've shown it
as the usual % of body mass, but it could be kg or pounds--the effect-size statistic
has the same value. The effect-size statistic is appropriate for studies of
population health, where differences or changes in means that impact the average
person are paramount.
Converting the difference to
a percent is one way to make the difference dimensionless, and therefore
more generic. Another important way is to express the difference as a fraction
or multiple of a standard deviation. Work out the difference between the means,
then divide it by the average standard deviation for the two groups. What you
end up with is the standardized difference in the means, a number that represents "how
many standard deviations" the two groups differ by. Look closely at the imaginary
example in the figure and work out the effect size for the difference in body
fat between boys and girls. Answer: one unit, or 1.0, or one standard deviation.
Note that the unit of measurement for body fat is irrelevant. I've shown it
as the usual % of body mass, but it could be kg or pounds--the effect-size statistic
has the same value. The effect-size statistic is appropriate for studies of
population health, where differences or changes in means that impact the average
person are paramount.