 Standard
Deviation
Standard
Deviation
The standard deviation is usually the best
measure of spread. It has a complicated definition: take the distance of each
number from the mean, square it, average the result, then take the square root.
In short, it's the root mean square of the distances (or differences) from mean.
It's usually abbreviated as SD in scientific journals and as s in stats books
and stats journals.
Actually, when you take the mean or average of the squares, you
have to divide by n - 1 (one less than the sample size). Dividing by
n gives you a biased estimate.
Obviously for large n it doesn't matter whether you use n or n-1, but
for n<20 it starts to make a difference. When using a calculator
to work out a standard deviation, press the
sn-1 button, not
sn.
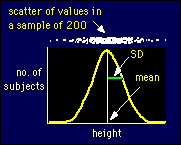 The
figure shows how big one SD looks on a frequency distribution for a
normally distributed variable like height. I've shown the frequencies
(number of subjects) as a continuous curve rather than as discrete
points for each value of height. The best way to think about the SD
is that about two-thirds of the values of a variable are found within
one SD each side of the mean.
The
figure shows how big one SD looks on a frequency distribution for a
normally distributed variable like height. I've shown the frequencies
(number of subjects) as a continuous curve rather than as discrete
points for each value of height. The best way to think about the SD
is that about two-thirds of the values of a variable are found within
one SD each side of the mean.
The standard deviation is sometimes expressed as a percent of
the mean, in which case it's known as a coefficient of variation. When
the SD and mean come from repeated measurements of a single subject, the resulting
coefficient of variation is an important measure
of reliability. This form of within-subject variation is particularly valuable
for sport scientists interested in the variability an individual athlete's performance
from competition to competition or from field test to field test. The coefficient
of variation of an individual athlete's performance is typically a few percent.
A measure of spread closely related to the SD is the
variance, which is simply the square of the SD. I can't show
you variance on a diagram. Statisticians prefer it to the SD, but
it's not much use for researchers.
Go to: Next
· Previous
· Contents ·
Search
· Home
webmaster=AT=sportsci.org
· Sportsci
Homepage
Last updated 4 July00
 The
figure shows how big one SD looks on a frequency distribution for a
normally distributed variable like height. I've shown the frequencies
(number of subjects) as a continuous curve rather than as discrete
points for each value of height. The best way to think about the SD
is that about two-thirds of the values of a variable are found within
one SD each side of the mean.
The
figure shows how big one SD looks on a frequency distribution for a
normally distributed variable like height. I've shown the frequencies
(number of subjects) as a continuous curve rather than as discrete
points for each value of height. The best way to think about the SD
is that about two-thirds of the values of a variable are found within
one SD each side of the mean.